Attenion is ALL YOU NEED!
前言
嗯最近期末没什么时间,简单写写,有时间再详细写写。
主要就是记录一下Transformer的一些重点,以及一些自己的理解。
模型结构
这是一个整体结构图
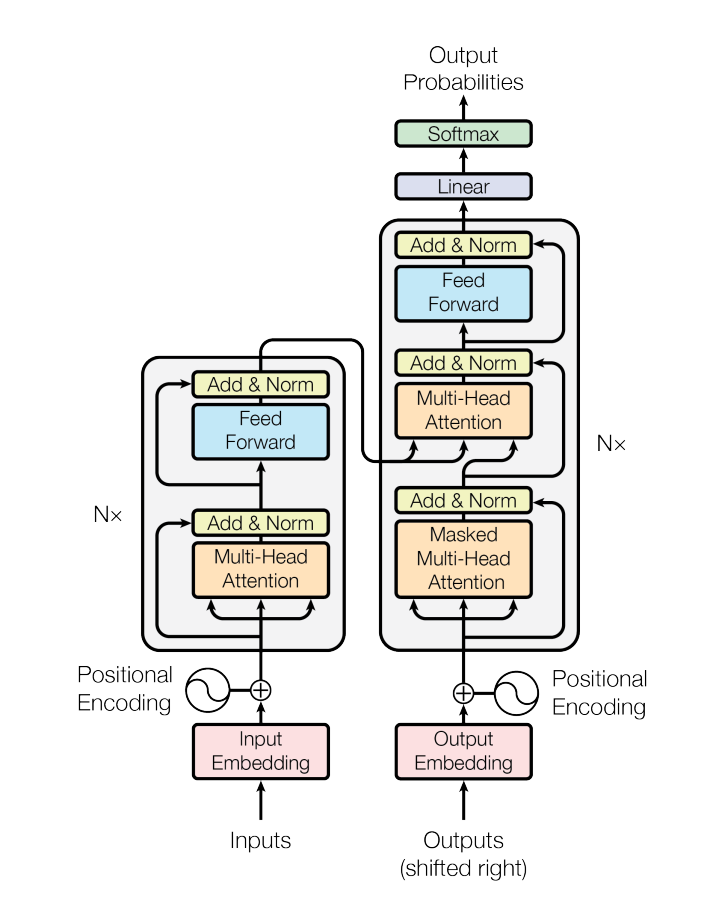
下文会回头再整体的说这个结构,现在先讲讲Attention。
Attention
讲到Transformer中怎么能不讲Attention呢? (毕竟,Attention is ALL YOU NEED!)
Attention机制是用来汇聚全局信息的一种方式。
尽管Attention机制在DL中并不是一个新概念,但是Transformer的出现使得Attention机制得到了广泛的关注。
不同的Attention有不同的注意力函数,最基本的注意力函数有基于点乘和基于加性的,Transformer中使用的是基于点乘的Attention机制。
确切来说,Transformer中使用注意力机制叫Scaled Dot-Product Attention。
注意力函数公式如下:
对于输入矩阵I,我们首先需要将其拆分为三个矩阵,分别是Query,Key和Value。这里我们通过可以学习三个不同的权重矩阵
接着,我们通过Query和Key的点乘,来计算Query和Key之间的相似度(显然点乘计算的就是向量的余弦相似度),然后通过softmax函数得到注意力权重,最后通过注意力权重与Value的相乘,来得到最终的输出。
嗯原文的解释是从一个Q开始的,不过显然是可以转为矩阵的并行运算的,所以我就不详细解释了。
为什么要除以
这个过程可以用下图表示:
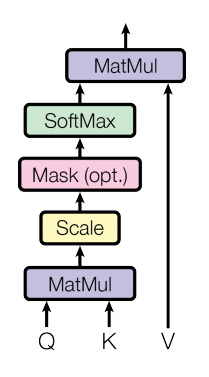
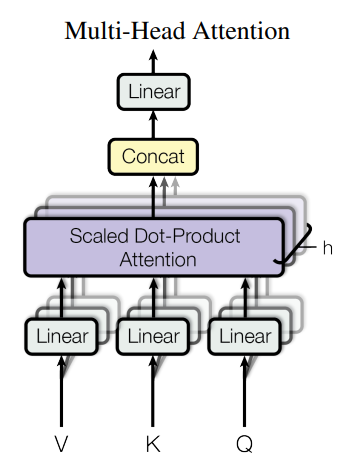
然后我们再来看看Multi-Head。
多头就是学习把Q,K,V投影为多组
这样可以允许我们学到更多的注意力方式,当然对应的数据量需求也会变大。
重回模型
然后回顾一下模型图,可以看到有三个地方用到了Attention:
Encoder中的Self-Attention: 这里的Q,K,V都来自同一个输入序列,所以叫Self-Attention。这样可以让每个位置都能关注到序列中的其他位置。
Decoder中的Masked Self-Attention: 这里也是Self-Attention,但是为了避免看到未来的信息,我们需要mask掉未来的位置(不然就不是自回归了)。具体来说就是在softmax之前把未来位置的attention score设为负无穷。
Decoder中的Cross-Attention: 这里的Q来自Decoder的输入,K和V来自Encoder的输出。这样可以让Decoder的每个位置都能关注到Encoder的所有位置。
这三种Attention各自发挥不同的作用:
- Encoder的Self-Attention让模型理解输入序列的内部关系
- Decoder的Masked Self-Attention让模型在生成时只依赖已生成的内容
- Cross-Attention则建立了Encoder和Decoder之间的桥梁,让Decoder能够根据输入信息来生成输出
注意到,Decoder中输入是原序列的shifted right,也就是把原序列右移一位,这样可以让Decoder在生成时符合时序,同时实现教师强制。
Positional Encoding
还有个值得一提点的是位置编码。
注意到,Transformer的注意力机制获取的是全局信息,但是没有考虑位置信息。
所以需要位置编码来告诉模型每个位置的信息。 原文中使用的是正弦和余弦函数来生成位置编码。
具体来说,对于序列中的每个位置
其中10000是一个缩放波长的因子。 这样可以给每个位置编码一个唯一的表示, 同时编码距离可以反应位置的远近。
Transformer与RNN/CNN
个人理解,可能会有错误,欢迎指正
在Transformer横空出世之前,主流的序列模型是RNN/CNN。
RNN通过直接的递归结构,考虑上一步的输出,和当前的信息,来实现序列的时序处理。
而Transformer使用注意力机制注意到全局序列信息,同时使用位置编码来注意到位置信息。
这是两者之间的区别。
对于CNN来说,从某种意义上来说,CNN可以看作是一种特殊的Transformer。
我们可以把CNN的卷积核看作是一种特殊的注意力机制。当然我们还可以从图的角度考虑,Transformer可以看作是一种特殊的GNN,而GCN和CNN之间的关系可以这样说:
in essence, message passing and convolution are operations to aggregate and process the information of an element’s neighbors in order to update the element’s value. In graphs, the element is a node, and in images, the element is a pixel. However, the number of neighboring nodes in a graph can be variable, unlike in an image where each pixel has a set number of neighboring elements.
或许可以参考:
- On the Relationship Between Self-Attention and Convolutional Layers
- Transformers are Graph Neural Networks
后记
有空下一篇可以写写GNN,然后ViT,然后一些注意力机制的变体。

