Direct-coupling analysis of residue coevolution captures native contacts across many protein families

---

BackGround

It has long been suggested that the resulting correlations among amino acid compositions at different sequence positions can be exploited to infer spatial contacts within the tertiary protein structure.

Crucial to this inference is the ability to disentangle direct and indirect correlations, as accomplished by the recently introduced direct-coupling analysis (DCA).

Here we develop a computationally efficient implementation of DCA, which allows us to evaluate the accuracy of contact prediction by DCA for a large number of protein domains, based purely on sequence information.

Here we will introduce mfDCA, an algorithm based on the mean-field approximation of DCA.

Methods

Data Extraction

For each family, the protein sequences are collected in one MSA denoted by $\{(A_1^a,A_2^a,...,A_L^a)|a=1,2,..,M\}$, where L denotes the number of MSA columns (i.e., the length of the protein domains). Alignments are local alignments to the Pfam HMM; because of the large number of proteins in each MSA, we refrained from refinements using global alignment techniques.

Sequence Statistics and Reweighting

The main inputs of DCA are reweighted frequency counts for single MSA columns and column pairs

重加权目的是为了纠正采样偏差，定义加权因子为 $\frac{1}{m^a}$ ，其中 $m^a$ 为与序列 $a$ 相同或序列同一性超过80%的序列数

定义有效序列数$M_{\text{eff}}$:

$$M_{\text{eff}}=\sum _{a=1}^M\frac{1}{m^a}$$

定义频率公式:

• 表示$\alpha$在所有MSA的i列出现的频率$$f_i(\alpha )=\frac{1}{M_{\text{eff}}+\lambda q^2}(\lambda +\sum _{a=1}^M\frac{1}{m^a}{\delta }_{\alpha ,A_i^a})$$
• 表示$\alpha$在所有MSA的i列且$\beta$在j列出现的联合频率$$f_{ij}(\alpha ,\beta )=\frac{1}{M_{\text{eff}}+\lambda q^2}(\lambda +\sum _{a=1}^M\frac{1}{m^a}{\delta }_{\alpha ,A_i^a}{\delta }_{\beta ,A_j^a})$$

其中 ${\delta }_{A,B}$ 表示如果 $A=B$ 则为1，否则为0；$q=21$ 表示包括空位在内的不同氨基酸数；$\lambda$ 是一个伪计数，用于统计稳定性。

此时我们可以直接计算出互信息MI(根据信息熵公式):

$$M{I}_{ij}=\sum _{A,B}{f}_{ij}(A,B)\ln \frac{f_{ij}(A,B)}{f_i(A)f_j(B)}$$

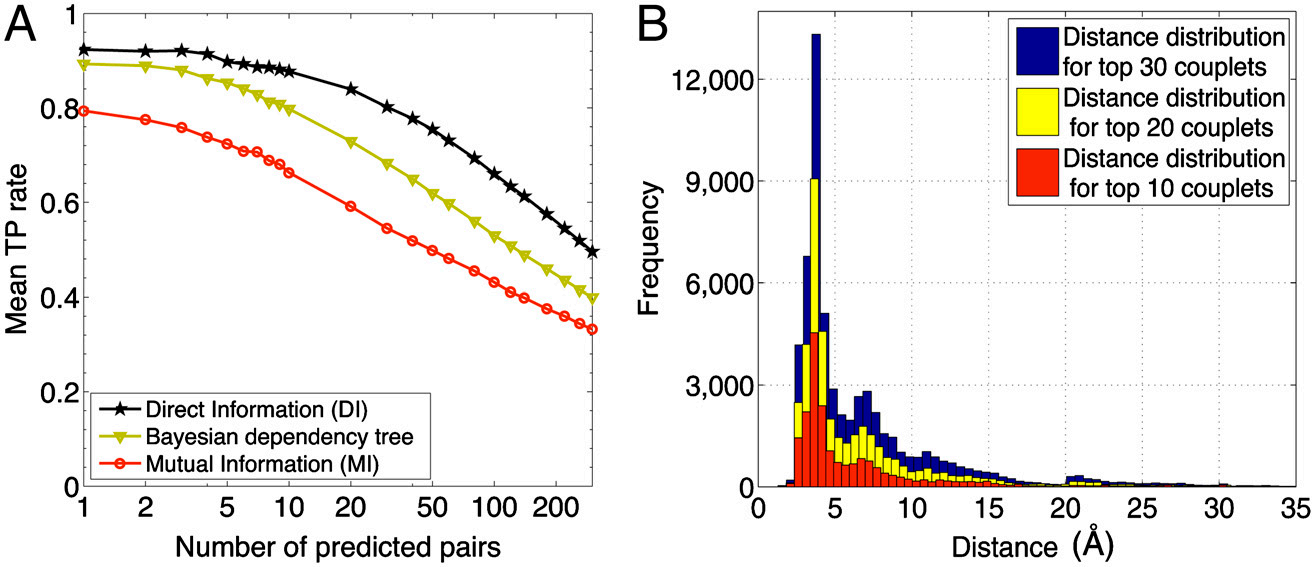
但是文中认为MI表示直接与间接相关性效果不太好,我们可以通过后续来推出更好的指标DI

DI与MI以及贝叶斯效果对比

待更新